simulation

Simulating Data with childpen

The childpen package includes a simulation engine designed to reproduce stylized patterns from the child-penalty literature—diverging earnings paths for women and men after the arrival of a first child.

This vignette shows how to generate data, and some stylistic facts on the DGP.

---

Basic usage

Draw data using the simulate_data function.

library(childpen)

N <- 100000
sim_data <- simulate_data(n_individuals = N)
sim_data |> tibble()
#> # A tibble: 2,100,000 × 6
#>       id female   age     D   Y_inf       Y
#>    <int>  <int> <int> <int>   <dbl>   <dbl>
#>  1     1      1    20    37  12181.  12181.
#>  2     1      1    21    37  15585.  15585.
#>  3     1      1    22    37 129489. 129489.
#>  4     1      1    23    37  74298.  74298.
#>  5     1      1    24    37 113396. 113396.
#>  6     1      1    25    37 101516. 101516.
#>  7     1      1    26    37 100317. 100317.
#>  8     1      1    27    37 428608. 428608.
#>  9     1      1    28    37 526744. 526744.
#> 10     1      1    29    37 210384. 210384.
#> # ℹ 2,099,990 more rows

The id column is the individual id. female is binary indicator, = 1 indicates females and = 0 indicates males. age indicates the age at which the earnings are observed. D is the treatment variable — age at first childbirth. Y_inf represents $Y_{i,a}(\infty)$, that is the potential earnings under never having a child. Y represents observed earnings, equal to potential earnings under having a child at $D$.

How as the DGP generated

The DGP is supposed to serve as a realistic DGP for simulations studies of child penalty applications.

The goal is to construct life-cycle earning profiles for the potential earnings under the observed treatment and under the counterfactual treatment of never having a child. The problem is that identifying these life-cycle patterns for counterfactual earnings is diffcult. So the DGP does some simplifying assumptions, to construct a process which creates life-cycle earnings, which are motivated by the empirical data.

1. Using Israeli administrative data, mean earnings for triplets (gender, treatment group, age) were estimated.
2. Mens mean earnings were fit with cubic polynomials.
3. Assume that men have zero treatment effect. Assign mean counterfactual earnings for men using means of observed outcomes.
4. Assume that womens’ mean counterfactual earnings, within treatment group, are equal to men up to age 27. Starting from age 28, inequality in counterfactual earnings increases by 0.025 per year.
5. Assume that the average treatment effect for women is a 30% drop at the time of treatment, and that women recover at a rate of 2% per year.

Example moments

Below I produce some graphs to construct intuition on the DGP behind the simulation.

First, for simplicity, treatment distribution is uniform, and treatment groups include 25-40.

sim_data |> 
  filter(age == D, female == 1) |>
  count(D)
#>     D    n
#> 1  25 3111
#> 2  26 3055
#> 3  27 3142
#> 4  28 3040
#> 5  29 3158
#> 6  30 3194
#> 7  31 3102
#> 8  32 3082
#> 9  33 3205
#> 10 34 3171
#> 11 35 3050
#> 12 36 3124
#> 13 37 3186
#> 14 38 3115
#> 15 39 3213
#> 16 40 3052

Second, treatment groups generally behave as:

1. Early treated (e.g., 25) - low selection (low ability / low human capital)
2. Mid treated (e.g. 30) - highest selection
3. Late treated (e.g. 35) - mid selection

sim_data |> 
  filter(D %in% c(25, 30, 35)) |> 
  group_by(female, D, age) |> 
  summarize(Y = mean(Y)) |> 
  ggplot(aes(x = age, y = Y, color = factor(D))) + 
  geom_point() + geom_line() +
  facet_wrap(facets = vars(female)) + 
  labs(x = "Age", y = "Mean Observed Earnings (Y)", color = "Treatment group", subtitle = "Facets = Male (0) and Female (1)")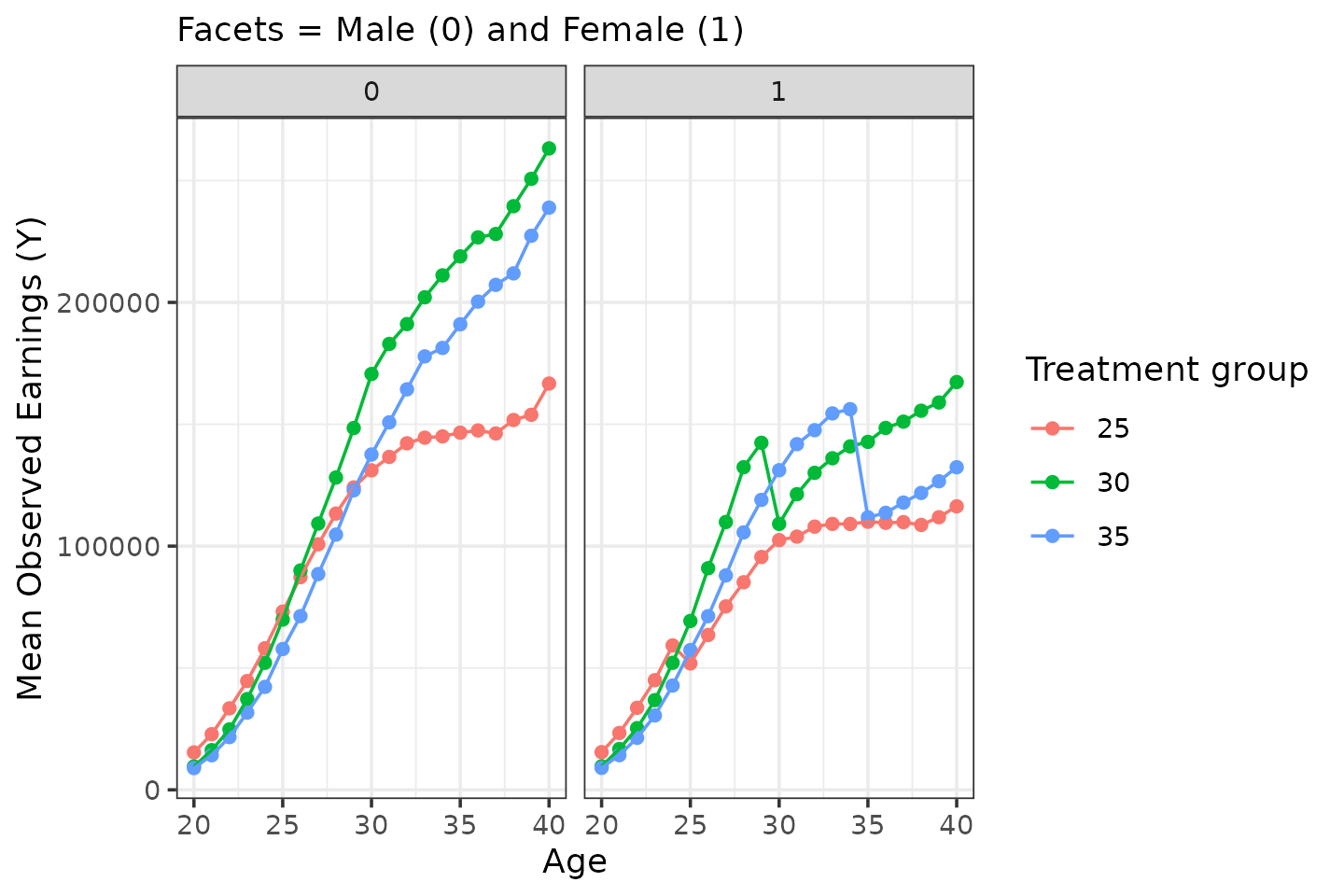

For men, zero treatment effect by construct. For women:

sim_data |> 
  filter(female == 1, 
         D %in% c(25, 30, 35)) |> 
  group_by(female, D, age) |> 
  summarize(Y = mean(Y), Y_inf = mean(Y_inf)) |> 
  ggplot(aes(x = age)) + 
  geom_point(aes(y = Y_inf, color = "Counterfactual")) + geom_line(aes(y = Y_inf, color = "Counterfactual")) +
  geom_point(aes(y = Y, color = "Observed")) + geom_line(aes(y = Y, color = "Observed")) +
  facet_wrap(facets = vars(D)) +
  labs(x = "Age", y = "Mean Earnings (Y / Y_inf)", color = "Type of Earnings", subtitle = "Facets = Treatment groups")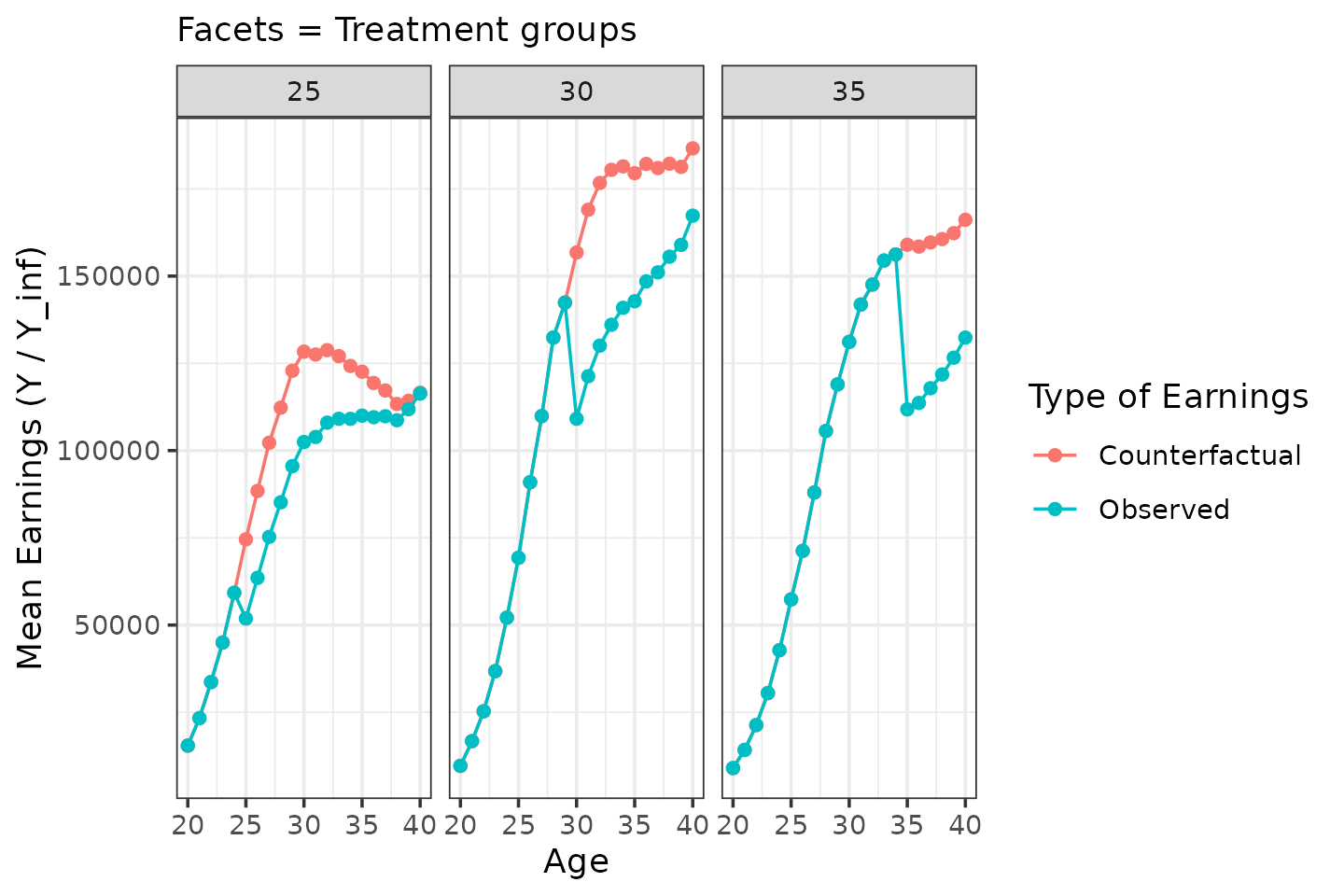

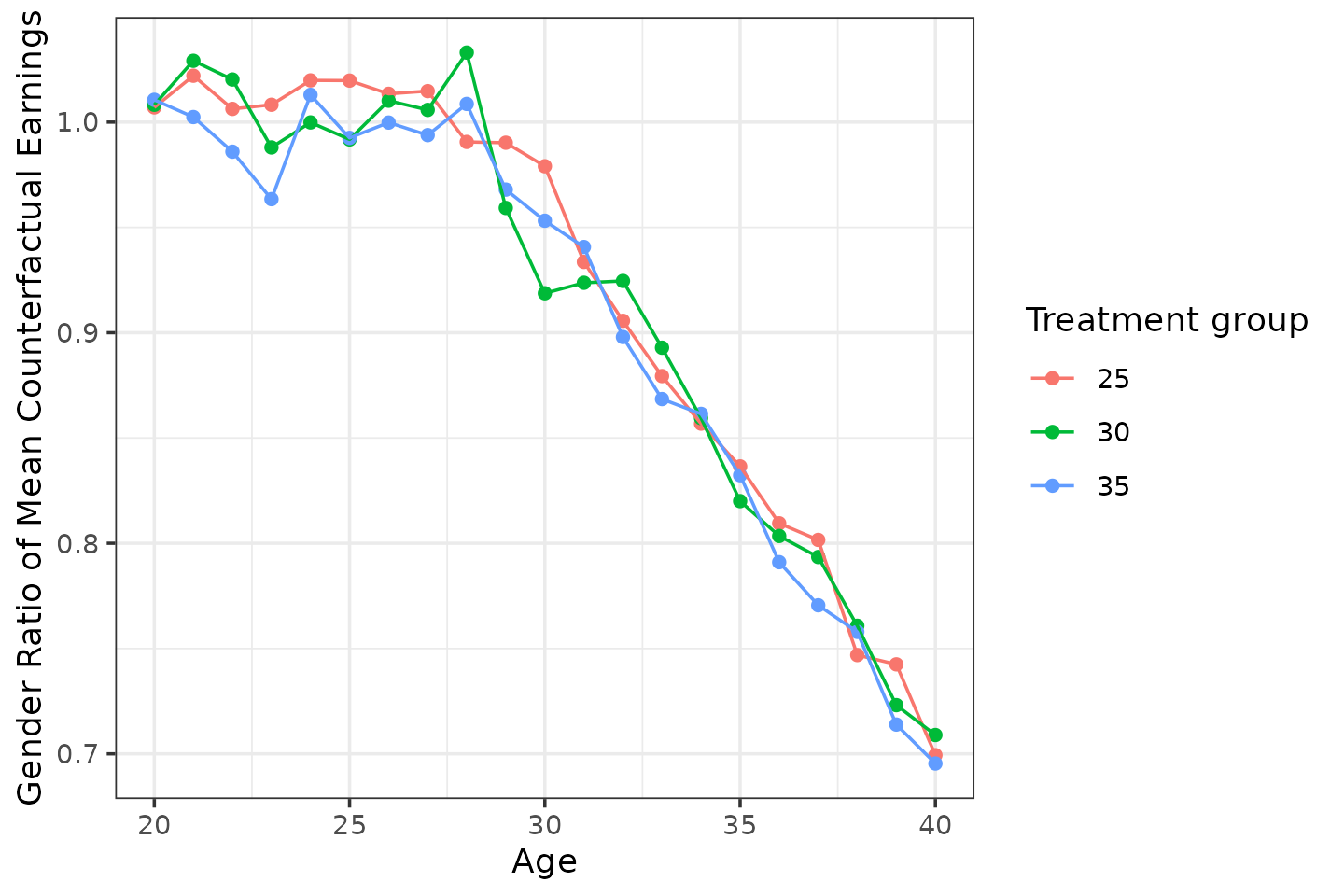
By construction, counterfactual gender inequality kicks in from age 28.

sim_data |> 
  filter(D %in% c(25, 30, 35)) |> 
  group_by(female, D, age) |> 
  summarize(Y_inf = mean(Y_inf)) |>
  pivot_wider(names_from = female, values_from = Y_inf, names_glue = "Y_inf_{female}") |> 
  mutate(rho = Y_inf_1 / Y_inf_0) |> 
  ggplot(aes(x = age, y = rho, color = factor(D))) + 
  geom_point() + geom_line()  +
  labs(x = "Age", y = "Gender Ratio of Mean Counterfactual Earnings", color = "Treatment group")