Skip to contents

DID-estimation

Source: vignettes/DID-estimation.Rmd
DID-estimation.Rmd

Overview

The aim of this vignette is show how to estimate difference in differences (DID) using closest-not-yet-treated control groups using childpen.

Simulate data

The package has a built in simulation function to draw data resembling child penalty studies.

library(childpen)

N <- 2000
data <- simulate_data(n_individuals = N)
data |> tibble()
#> # A tibble: 42,000 × 6
#>       id female   age     D  Y_inf      Y
#>    <int>  <int> <int> <int>  <dbl>  <dbl>
#>  1     1      1    20    37  7337.  7337.
#>  2     1      1    21    37 10446. 10446.
#>  3     1      1    22    37 25834. 25834.
#>  4     1      1    23    37 38254. 38254.
#>  5     1      1    24    37 60609. 60609.
#>  6     1      1    25    37 46775. 46775.
#>  7     1      1    26    37 26192. 26192.
#>  8     1      1    27    37 32976. 32976.
#>  9     1      1    28    37 27096. 27096.
#> 10     1      1    29    37 75304. 75304.
#> # ℹ 41,990 more rows

DID Estimands and Estimators

DIDs starting point is a 2×22\times2 comparison. We consider some treatment group dd (e.g., 25), and want to effects for some target age aa (e.g., 30). The pre-treatment period is initially set to d−1d-1 (e.g., 24), but this can be changed in childpen using the argument pre. The control group d′d^\prime is always set to the closest-not-yet-treated group, i.e., childpen automatically sets d′=a+1d^\prime=a+1. For example, for target age a=30a=30, the closest group that is not yet treated is parents that had their first child at 31.

DID calculates average potential outcomes in the counterfactual without childbirth by adding to the treatment group dd the trend for the control group d′d^\prime between ages d−1d-1 and aa. Let G∈{f,m}G\in\{f,m\} be female or male gender, DD the age at first childbirth, YY the outcome. We write the DID counterfactual average potential outcomes as δAPO(g,d,d′,a)=𝔼[Yd−1∣G=g,D=d]+𝔼[Ya−Yd−1∣G=g,D=d′]. \delta_{\mathrm{APO}}(g,d,d^\prime,a)=\mathbb{E}[Y_{d-1}\mid G=g, D=d]+\mathbb{E}[Y_a-Y_{d-1}\mid G=g, D=d^\prime]. The DID average treatment effect (in levels) for defined for gender gg and treatment group dd is written as δATE(g,d,d′,a)=𝔼[Ya∣G=g,D=d]−δAPO(g,d,d′,a) \delta_{\mathrm{ATE}}(g,d,d^\prime,a)=\mathbb{E}[Y_a\mid G=g, D=d]-\delta_{\mathrm{APO}}(g,d,d^\prime,a) Finally, in the child penalty application, many studies consider a normalized target, which divides the level effects by the estimated counterfactual. DID can calculate that via δθ(g,d,d′,a)=δATE(g,d,d′,a)δAPO(g,d,d′,a) \delta_{\theta}(g,d,d^\prime,a)=\frac{\delta_{\mathrm{ATE}}(g,d,d^\prime,a)}{\delta_{\mathrm{APO}}(g,d,d^\prime,a)} All δ\deltas are descriptive estimands. Descriptive, in the sense that the do not include potential outcomes, only observable data. Estimands, in the sense that they include population expectations.

The equivalent estimators simply replace population estimands with sample means. Since all estimators are combinations of simple averages, it is easy to construct influence functions with which variances can be estimated. For more details, see the estimation appendix in the paper.

Multiple treatment group analysis

We will now do the main heavy lifting. Say you want to estimate DID with closest-not-yet-treated control groups. This will be many 2×22\times2s. childpen easily allows it using the wrapper function below, multiple_treatment_group_analysis(). Note that the column names of the data are the same as the default for the function, so no need to input explicitly.

res = multiple_treatment_group_analysis(data = data,
                                  treatment_groups = 25:30, # which treatment groups to run in the analysis
                                  periods_post = 5, # estimate results for post periods 0:5
                                  periods_pre = NULL, # estimate pre-trend diagnostics, set to NULL to omit from estimation
                                  max_age = 40, # dont estimate results if age is above 40
                                  min_age = 20, # dont estimate results if age is below 20
                                  pre = 1, # use 1 period before treatment, can make further away if anticipation is conern
                                  verbose = FALSE # set to TRUE to output progress (i like to time loops) set to FALSE to omit messages
                                  )

Only DID, plot post-treatment results

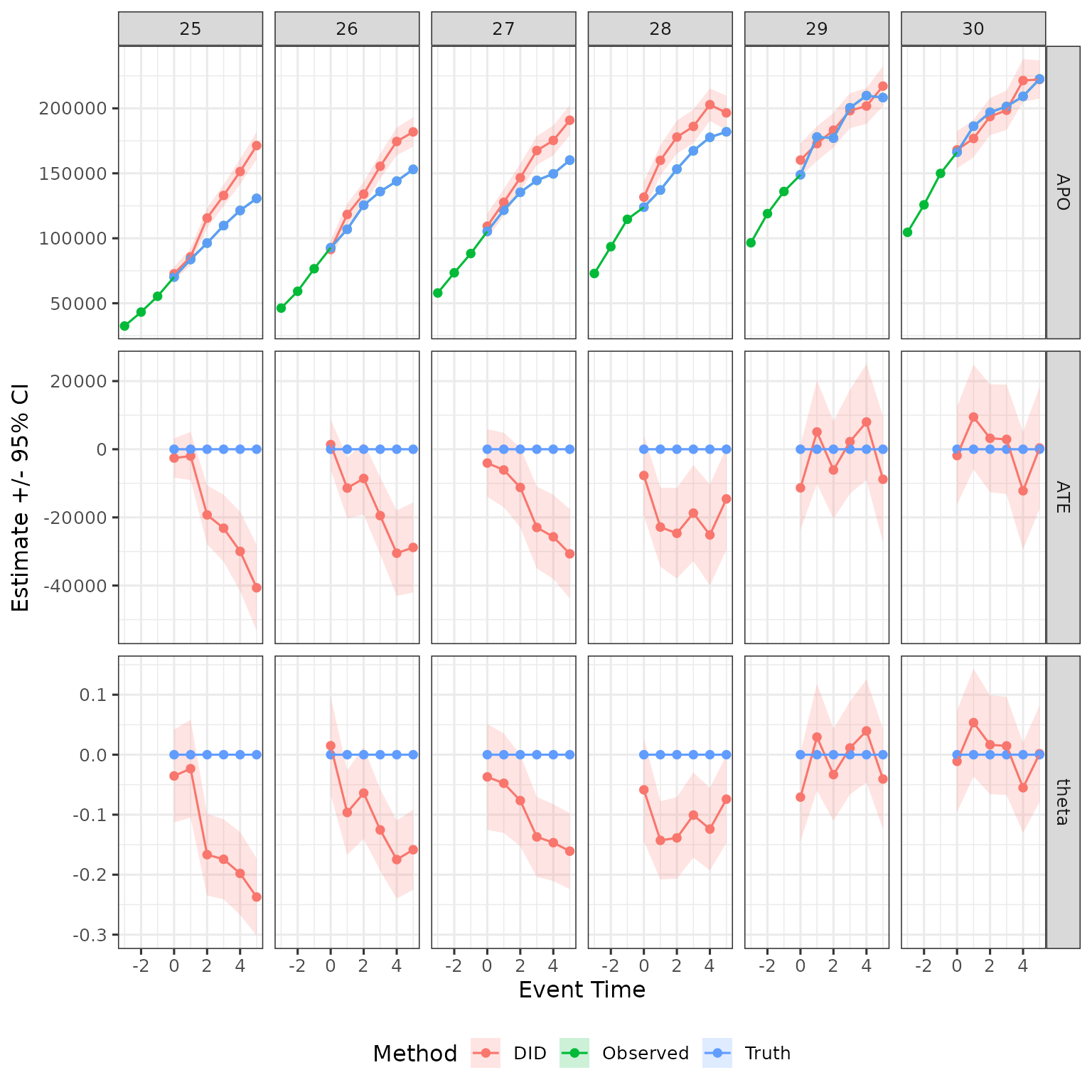
The above function outputs results for all estimation methods discussed in the paper. Let save only DID results, and graph them. For benchmarking, I also add to the plots the mean observed earnings from the raw data.

obs_tidy = data |> 
  mutate(event_time = age - D) |> 
  rename(d = D) |> 
  group_by(female, d, event_time) |> 
  summarize(est = mean(Y)) |> 
  mutate(estimand = "APO", method = "Observed") |> 
  filter(event_time %in% -3:5, d %in% 25:30)

plot_data = res |> 
  filter(method %in% c("DID_Female", "DID_Male")) |> 
  mutate(female = ifelse(method == "DID_Female", 1, 0)) |> 
  select(d, event_time, estimand, female, est, ci_l, ci_h) |> 
  mutate(method = "DID")

plot_data = plot_data |> 
  dplyr::bind_rows(obs_tidy)

plot_data |> 
  filter(female == 1) |> 
  ggplot(aes(x = event_time, y = est, ymin = ci_l, ymax = ci_h, color = method, fill = method)) + 
  geom_ribbon(color = NA, alpha = .2) +
  geom_point() + geom_line() + 
  facet_grid(cols = vars(d), rows = vars(estimand), scales = "free") + 
  labs(x = "Event Time", y = "Estimate +/- 95% CI", color = "Method", fill = "Method") + 
  theme(legend.position = "bottom")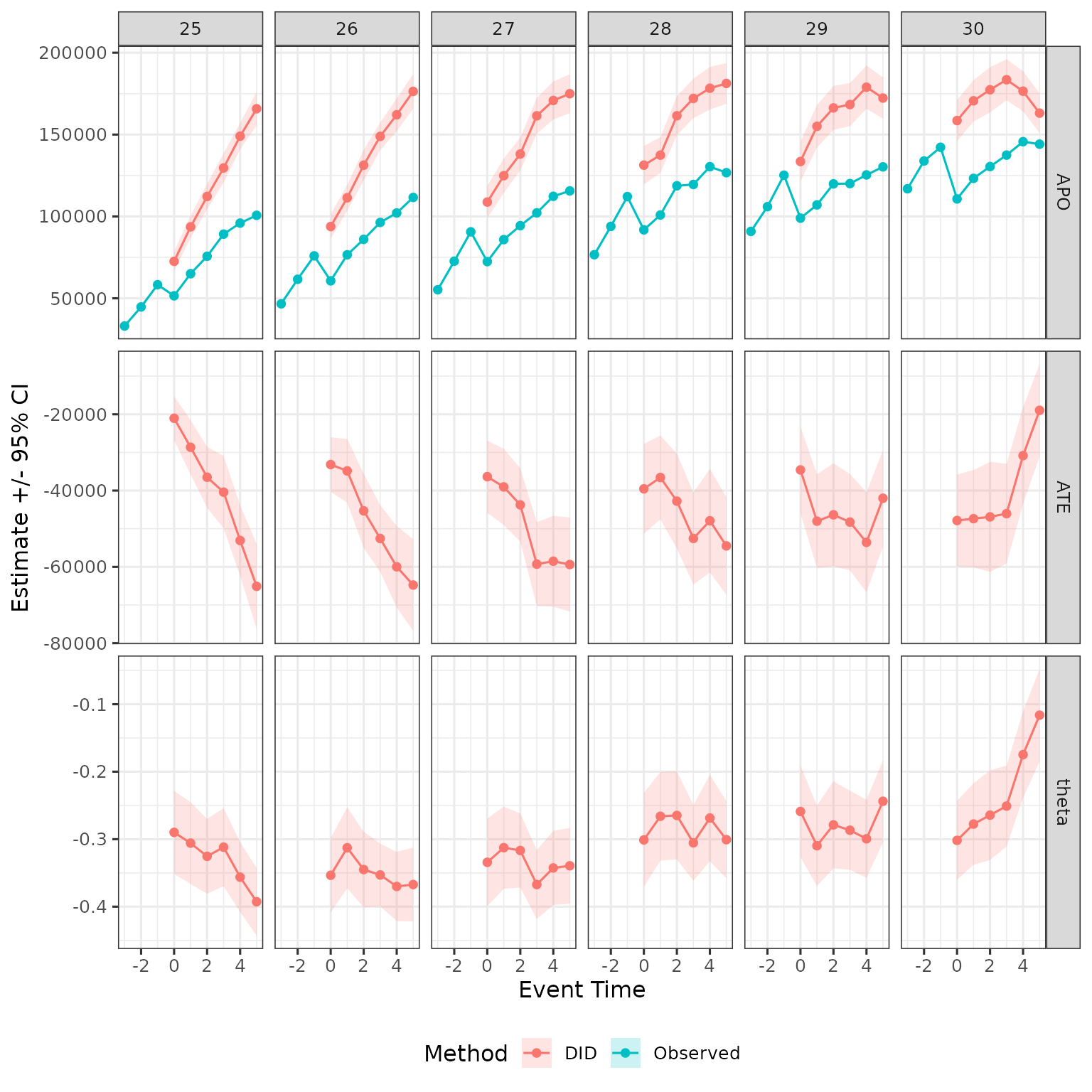

Compare to real effects in the simulation

The simulation offers also potential outcomes so we can see effect: Null for fathers and 30% decline with some constant recovery for mothers.

PO_tidy = data |> 
  mutate(event_time = age - D) |> 
  rename(d = D) |> 
  group_by(female, d, event_time) |> 
  summarize(APO_obs = mean(Y), APO = mean(Y_inf)) |> 
  mutate(ATE = APO_obs - APO, 
         theta = ATE / APO) |> 
  filter(event_time %in% 0:5, d %in% 25:30) |> 
  select(-APO_obs) |> 
  pivot_longer(
    !c(female, d, event_time), names_to = "estimand", values_to = "est"
  ) |> 
  mutate(method = "Truth")

plot_data = plot_data |> 
  dplyr::bind_rows(PO_tidy)

plot_data |> 
  filter(female == 1) |> 
  ggplot(aes(x = event_time, y = est, ymin = ci_l, ymax = ci_h, color = method, fill = method)) + 
  geom_ribbon(color = NA, alpha = .2) +
  geom_point() + geom_line() + 
  facet_grid(cols = vars(d), rows = vars(estimand), scales = "free") + 
  labs(x = "Event Time", y = "Estimate +/- 95% CI", color = "Method", fill = "Method") + 
  theme(legend.position = "bottom")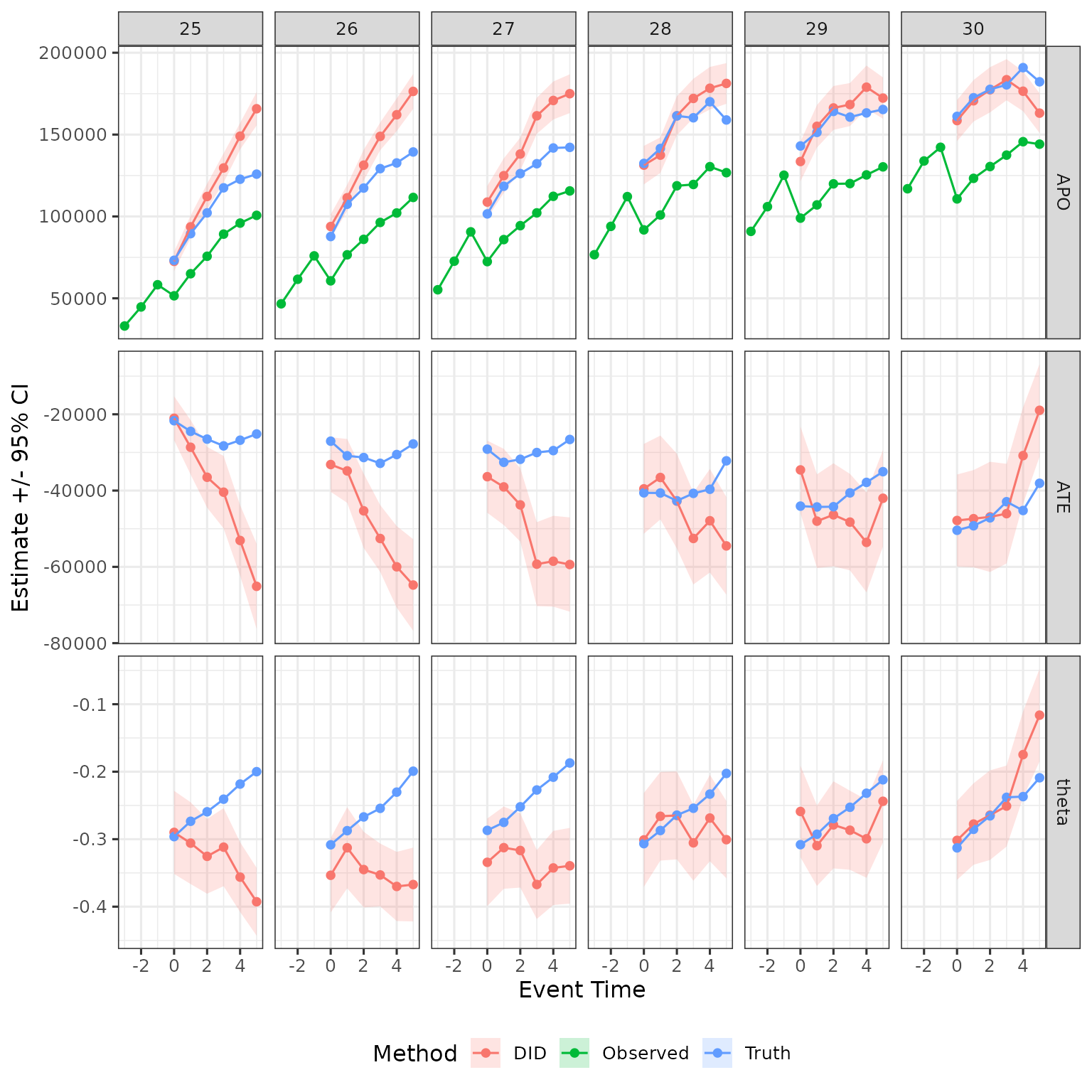

The intuition for this result, discussed in the paper, is that later treatment groups are positively selected compared to earlier treatment groups, and hence DID is overstating treatment effects for those groups.

For completness, show for men as well 

plot_data |> 
  filter(female == 0) |> 
  ggplot(aes(x = event_time, y = est, ymin = ci_l, ymax = ci_h, color = method, fill = method)) + 
  geom_ribbon(color = NA, alpha = .2) +
  geom_point() + geom_line() + 
  facet_grid(cols = vars(d), rows = vars(estimand), scales = "free") + 
  labs(x = "Event Time", y = "Estimate +/- 95% CI", color = "Method", fill = "Method") + 
  theme(legend.position = "bottom")

Validation tests

For a discussion on how to perform validation tests, and what type of tests are correct for this type of estimation, see the validation test vignette.